3D Functional Parameters
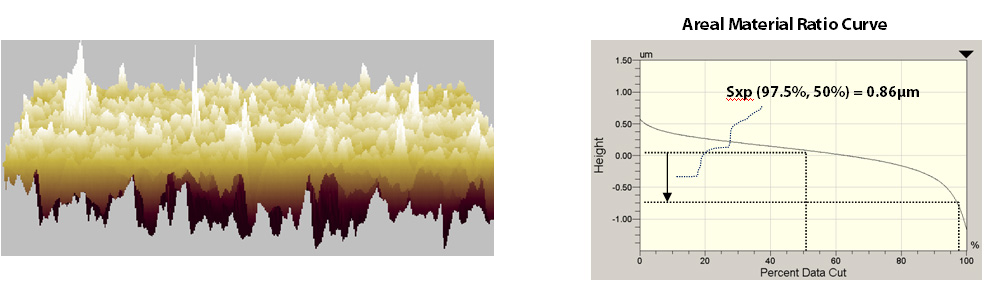
Sxp (p,q) Peak Extreme Height
The Peak Extreme Height, Sxp (p,q), is a measure of the difference in heights on the surface from the areal material ratio value of “p” and the areal material ratio of “q”. The default value for “p” is 97.5% and the default value for “q” is 50%.
Application
Assuming a surface was worn or modified such that the resulting material area was 50%, Sxp (97.5%, 50%) indicates the depth of the remaining material to the lowest regions of the texture. Thus Sxp (97.5%,50%) may be used to determine the depth of material available after 50% or the surface has either been removed or deformed to a plateau-like structure. By changing the values of “p” and “q”, Sxp (p,q) may be used to control other aspects of the texture.
As another example, Sxp (90%, 10%) may be used to control the overall “peak-to valley” height of the surface by not accounting for the top 10% of the surface which may likely be easily deformed/worn and the bottom 10% which may be easily filled in during initial surface interactions.
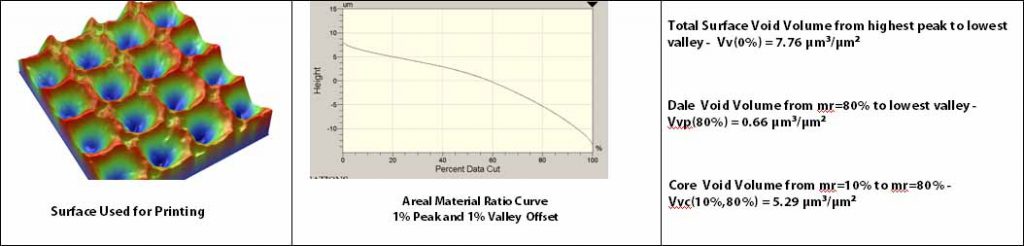
Vv(mr) (Void Volume), Vvv(p) (Dale Void Volume), Vvc(p,q) (Core Void Volume)
Vv(mr), the Void Volume, is the volume of space bounded by the surface texture from a plane at a height corresponding to a chosen “mr” value to the lowest valley. “mr” may be set to any value from 0% to 100%.
Vvv(p), the Dale Void Volume, is the volume of space bounded by the surface texture from a plane at a height corresponding to a material ratio (mr) level, “p” to the lowest valley. The default value for “p” is 80% but may be changed as needed.
Vvc(p,q), The Core Void Volume, is the volume of space bounded by the texture at heights corresponding to the material ratio values of “p” and “q”. The default value for “p” is 10% and the default value for “q” is 80%.
Application
Vv(mr), Vvv(p) and Vvc(p,q) all indicate a measure of the void volume provided by the surface between various heights as established by the chosen material ratio(s) values. Thus these three void volume parameters indicate how much fluid would fill the surface (normalized to the measurement area) between the chosen material ratio values. For example, a Vv(25%) = 0.5 µm3/µm2 in (note how the units µm3/µm2 reduce to µm) that a 0.5 µm thick film over the measurement area would provide the same volume of fluid as needed to fill the measured surface from a height corresponding to mr=25% to the lowest valley.
The void volume parameters are useful when considering fluid flow, coating applications and debris entrapment. A new surface may be specified by Vv(0%) which would indicate the total initial void volume provided by the texture. The Core Void Volume , Vvc, may be useful to establish how much core space is available once a surface has been run-in resulting in decreased peak heights . The Dale Void Volume, Vvv(p) may be useful in indicating the potential remaining volume after significant wear of a surface has resulted.
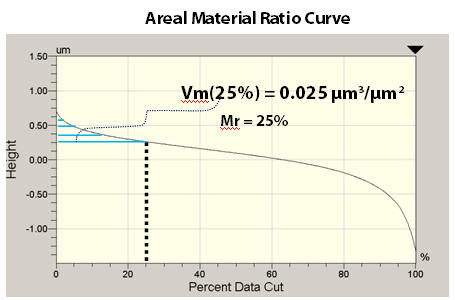
Vm(mr) (Material Volume), Vmp(p) (Peak Material Volume), Vmc(p,q) (Core Material Volume)
Vm(mr), the Material Volume, is the volume of material comprising the surface from the height corresponding to mr to the highest peak of the surface. “mr” may be set to any value from 0% to 100%.
Vmp(p), the Peak Material Volume, is the volume of material comprising the surface from the height corresponding to a material ratio level, “p”, to the highest peak. The default value for “p” is 10% but may be changed as needed.
Vmc(p,q), the Core Material Volume, is the volume of material comprising the texture between heights corresponding to the material ratio values of “p” and “q”. The default value for “p” is 10% and the default value for “q” is 80% but may be changed as needed.
Application
Vm(mr), Vmp(p) and Vmc(p,q) all indicate a measure of the material forming the surface at the various heights down from the highest peak of surface or between various heights as defined for Vmc(p,q).
For example, a Vm(10%) =0.35µm3/µm2 would indicate (note how the units µm3/µm2 reduce to µm) that a layer 0.35µm thick of material over the measured cross section would account for all the material from the highest peak to the 10% point on the bearing area curve.
The various Material Volume parameters are useful to understand how much material may be worn away for a given depth of the bearing curve (i.e. Vmp(p)) and how much material is available for load support once the top levels of a surfaces are worn away (i.e. Vmc(p,q)). For sealing applications, Vmp(p) may provide insight into the amount of material available for seal engagement whereas Vvc(p.q) (see above) may then provide information about the resulting void volume for fluid entrapment or leakage.

