Sku
For the discussions that follow, Z(x,y) is the function representing the height of the surface relative to the best fitting plane, cylinder, or sphere. Note that the “a” used in the following integral expressions implies that the integration is performed over the area of measurement and then normalized by the cross-sectional area “A” of the measurement.
Ssk (Skewness) and Sku (Kurtosis)
Ssk and Sku are the Skewness and Kurtosis of the 3D surface texture respectively. Figuratively, a histogram of the heights of all measured points is established and the symmetry and deviation from an ideal Normal (i.e. bell curve) distribution is represented by Ssk and Sku. Mathematically, the Ssk and Sku are evaluated as follows:
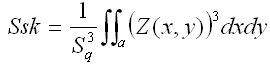
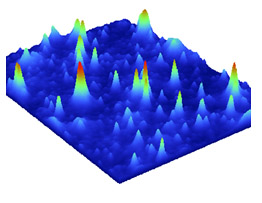
Surface with multiple peaks Ssk = 3.20 Sku = 18.71.
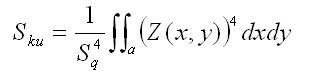
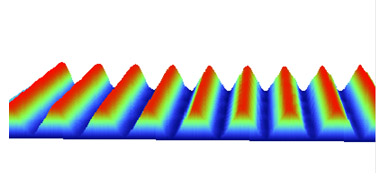
Periodic Texture Ssk = 0.16 Sku= 1.63.
Application
Ssk represents the degree of symmetry of the surface heights about the mean plane. The sign of Ssk indicates the predominance of peaks (i.e. Ssk>0) or valley structures (Ssk<0) comprising the surface. Sku indicates the presence of inordinately high peaks/ deep valleys (Sku>3.00) or lack thereof (Sku<3.00) making up the texture. If the surface heights are Normally distributed (i.e. bell curve) then Ssk is 0.00 and Sku is 3.00. Surfaces described as gradually varying, free of extreme peaks or valley features, will tend to have Sku <3.00. Ssk is useful in specifying honed surfaces and monitoring for different types of wear conditions. Sku is useful for indicating the presence of either peak or valley defects which may occur on a surface. Since Ssk and Sku involve the higher order powers of the surface heights, one must make enough measurements to provide statistically significant values and/or properly select filtering bandwidths to eliminate erroneous peaks or valleys.
