The terms “roughness,” “waviness” and “form” are used everywhere in discussions of surface texture. But do we really understand how they are defined?
For many years I have used an image of a favorite mountain of mine, Picacho Peak, which rises starkly from the desert between Tucson and Phoenix, Arizona. There is a great hike up and around the mountain which earns you a view of the desert floor for miles in any direction.

I like to use the image of Picacho as a way of explaining the meaning of the three surface texture regimes. Most people tend to understand innately that “roughness” refers to finer spaced surface texture features, while “waviness” is more of an undulation, and “form” is the gross shape of a surface, or of the object whose surface we are viewing.
However, many people, even those who have worked around surface texture for years, tend to think that there is a number—a fixed value—below which we consider texture to be “roughness” and above which we call it “waviness.” We might see a number such as 0.8 mm and immediately interpret it as “the cutoff between waviness and roughness.” But this is far from accurate.
Roughness and Waviness…Defined by the Application
The distinction between roughness and waviness is intended to help us understand the makeup of a surface’s texture and, more important, to understand how the texture will affect the surface’s performance in a given application. Roughness and waviness determine many aspects of surface functionality, from how well a coating may protect to how well a contact lens will help us see better. We design surfaces to perform functions—and we specify the surface texture to optimize performance in those functions.
How we define “roughness” and “waviness,” then, must also be based on the intended function. This is where the image of Picacho Peak comes into play.
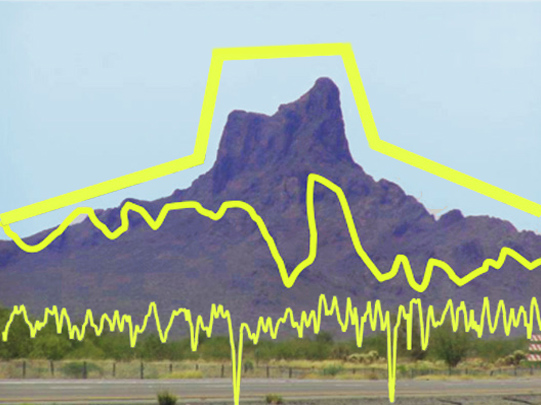
I think of the trail up Picacho as my surface. How difficult it is to hike, and how well my hiking abilities are suited to it, is the function that I need to understand. The overall form of the mountain is, of course, critical (“The peak is 1614 feet high—I need to be prepared to break a sweat.”) But I also need to know about the waviness (“The trail goes over several peaks and down into several canyons…it is longer than it looks”). And, I need to know about the trail surface itself—the roughness—to know which shoes to wear (“There are a lot of loose rocks, so I need boots that support my ankles”).
In the case of the hike, the roughness, waviness and form are on human-sized scales. The rocks on the path could be measured in inches, the waviness in feet and the form in hundreds of feet, say. For the hiking application, those are the lateral scales that matter.
On the other hand, say I am trying to measure a very smooth surface, such as that of a telescope mirror. In this case defining roughness length scale in terms of inches, or waviness length scale in terms of feet, would be utterly useless. The average roughness amplitude of the polished mirror is likely on the order of nanometers rather than inches! Thus I may need to measure the texture along length scales measured in micrometers (1 micrometer is equal to about 0.025″). Quite a bit smaller than the rocks on the trail.
When we specify surface texture, we need to define roughness and waviness in terms of the application at hand. And, we need a method for communicating these numbers so that everyone in the process can measure and interpret the values in the same way.
Cutoff wavelengths define roughness and waviness
We define roughness and waviness by specifying the ranges of “spatial wavelengths” within the texture that matter to us. Spatial wavelengths are lateral measurements rather than heights; shorter wavelengths are toward the roughness end of the spectrum, while longer wavelengths may be considered waviness.
We state what we mean by roughness or waviness by specifying a “Short Cutoff” (λs) and a “Long Cutoff” (λc) to define the interesting range of wavelengths. Once we have defined the range, then we can specify the aspects of that range (average roughness (Ra) , RMS roughness (Rq), etc) that we need to measure and control.
For our hiking example, we know that we need to understand the rockiness of the path, the rise and fall of the trail and the overall shape of the mountain. We might specify the roughness regime (rockiness) with a Short Cutoff (λs) value of 1 inch and a Long Cutoff (λc) of 10 inches. This would give us a good sense of the number and size of ankle-busting rocks on the trail. We might define waviness as the values between λsw = 10 feet and λcw = 200 feet, which would indicate how much the trail rises and falls. Values above 200 feet would describe the overall form of the mountain, which would tell us whether we are fit enough to attempt the climb at all.
Considering the telescope mirror, the roughness regime might be between λs = 0.001 mm and λc =0.080 mm, with waviness defined by λsw = 0.080 mm and λcw = 0.800 mm. Whether polishing a mirror or hiking a mountain we can still speak in terms of roughness and waviness, even though the cutoff values may differ by many orders of magnitude.
We must define the cutoffs for the data to be meaningful!
All prominent standards, including the ASME B46.1 2009 standard, require that cutoff wavelengths be specified in order to make the measurement results meaningful. When the values are not stated, the standards provide guidelines for setting the values. These may or may not be applicable for our application, but they will at least make sure we correctly interpret the results.
There are many considerations to address regarding the selection of cutoff frequencies. In an upcoming article we will delve deeper into some of these considerations.
