3D Height (Amplitude) Parameters
For the discussions that follow, Z(x,y) is the function representing the height of the surface relative to the best fitting plane, cylinder, or sphere. Note that the “a” used in the following integral expressions implies that the integration is performed over the area of measurement and then normalized by the cross-sectional area “A” of the measurement.
Sa and Sq
Sa and Sq are the Average Roughness and Root Mean Square Roughness are evaluated over the complete 3D surface respectively. Mathematically, Sa and Sq are evaluated as follows:
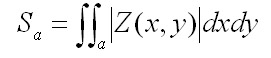
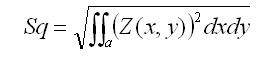
Application
The Sa and Sq parameters represent an overall measure of the texture comprising the surface. Sa and Sq are insensitive in differentiating peaks, valleys and the spacing of the various texture features. Thus Sa or Sq may be misleading in that many surfaces with grossly different spatial and height symmetry features (e.g., milled vs. honed) may have the same Sa or Sq, but function quite differently. The figure above demonstrates two very different surfaces with identical Sa and Sq values, indicating the insensitivity of the Sa and Sq parameters. Nonetheless, once a surface type has been established, the Sa and Sq parameters may be used to indicate significant deviations in the texture characteristics. Sq is typically used to specify optical surfaces and Sa is used for machined surfaces.
Ssk (Skewness) and Sku (Kurtosis)
Ssk and Sku are the Skewness and Kurtosis of the 3D surface texture respectively. Figuratively, a histogram of the heights of all measured points is established and the symmetry and deviation from an ideal Normal (i.e. bell curve) distribution is represented by Ssk and Sku. Mathematically, the Ssk and Sku are evaluated as follows:
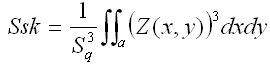
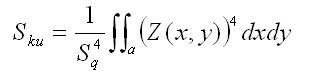
Application
Ssk represents the degree of symmetry of the surface heights about the mean plane. The sign of Ssk indicates the predominance of peaks (i.e. Ssk>0) or valley structures (Ssk<0) comprising the surface. Sku indicates the presence of inordinately high peaks/ deep valleys (Sku>3.00) or lack thereof (Sku<3.00) making up the texture. If the surface heights are Normally distributed (i.e. bell curve) then Ssk is 0.00 and Sku is 3.00. Surfaces described as gradually varying, free of extreme peaks or valley features, will tend to have Sku <3.00. Ssk is useful in specifying honed surfaces and monitoring for different types of wear conditions. Sku is useful for indicating the presence of either peak or valley defects which may occur on a surface. Since Ssk and Sku involve the higher order powers of the surface heights, one must make enough measurements to provide statistically significant values and/or properly select filtering bandwidths to eliminate erroneous peaks or valleys.
Sp (Max Peak Height), Sv Max Valley Depth) and Sz (Max Height of Surface)
Sp, Sv, and Sz are parameters evaluated from the absolute highest and lowest points found on the surface. Sp, the Maximum Peak Height, is the height of the highest point, Sv, the Maximum Valley Depth, is the depth of the lowest point (expressed as a negative number) and Sz the Maximum Height of the Surface), is found from Sz = Sp – Sv.
Note: earlier standards referred to Rz as a average of the 10 highest to 10 Lowest Points and other variations. The ISO community agreed for the newer standard, ISO 25178-2 to establish Sz as strictly the peak to valley height over a areal measurement.


Application
Since Sp, Sv, and Sz are found from single points, they tend to result in unrepeatable measurements. Thus when using these three parameters, one must properly set spatial filtering bandwidths to eliminate erroneous peaks/valleys and average multiple measurements at random locations along the sample, to obtain a statistically significant result. Typical applications for Sz may include sealing surfaces and coating applications. Sp may find application when considering surfaces that will be used in a sliding contact application. Sv may find application when valley depths relating to fluid retention may be of concern such as for lubrication and coating systems.
