Sdr
Sdr is the Developed Interfacial Area Ratio. It is the percentage of surface area that the surface texture adds to an ideally smooth and flat surface of the same cross-sectional area as the measurement region.

An Sdr of 0.023% means that if you have an ideally smooth surface, then you add the surface texture, the surface area will be 0.023% larger.
Sdr can be calculated over a particular band of spatial wavelengths that matter for our application. We define that band by applying a short and long filter. If, say, we know that a coating is most affected by features between 0.2 µm and 2.0 µm, we can apply a 0.2 µm short filter and a 2.0 µm long filter, then calculate Sdr over just that band.
Surface area and Sdr
Surface area impacts how well a coating will adhere, how well a liquid will wet a surface, how well ink will fill a print roller, etc. If we measure the size of the surface area, however, the result will depend on the lateral scale size of the features that we include in our measurement.
Imagine trying to measure the length of the coast of Florida. You’ll get one answer if you set out on a cruise ship and follow the shoreline. But in a smaller vessel, you could sail into every bay, so your measurement would be longer. If you swim into every cove, or step around every rock and pebble on the shore, the results would be longer yet.
The same is true of surface area: we will get progressively larger numbers as we include smaller and smaller lateral scales (spatial wavelengths) in the analysis. For a 2D profile, like the one below, we will get different answers if we use a shorter and longer ruler. The smaller the features we include in the measurement, the longer the overall length we will measure.
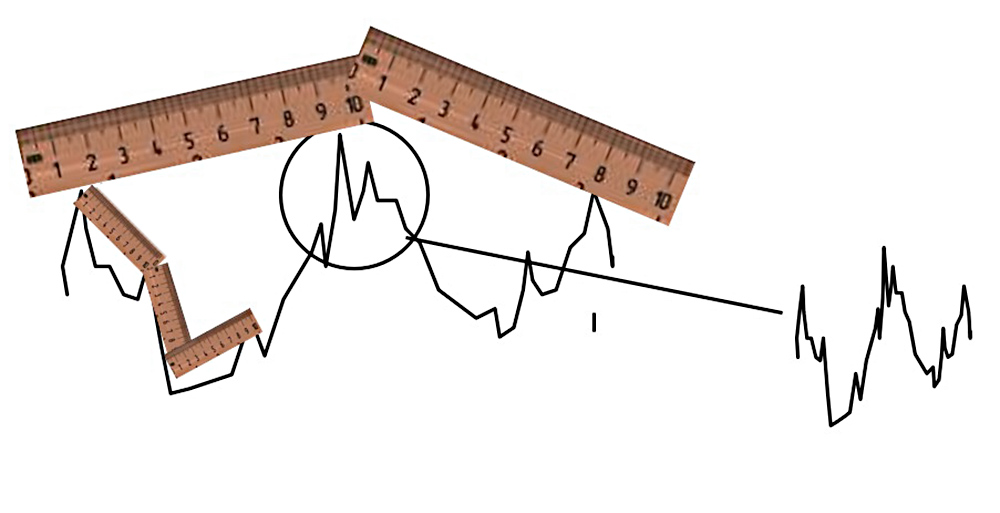
For areal (3D) data, we determine the overall surface area by “tiling” the surface with triangles, as in the image below. The smaller the tiles, the larger the surface area we will measure.
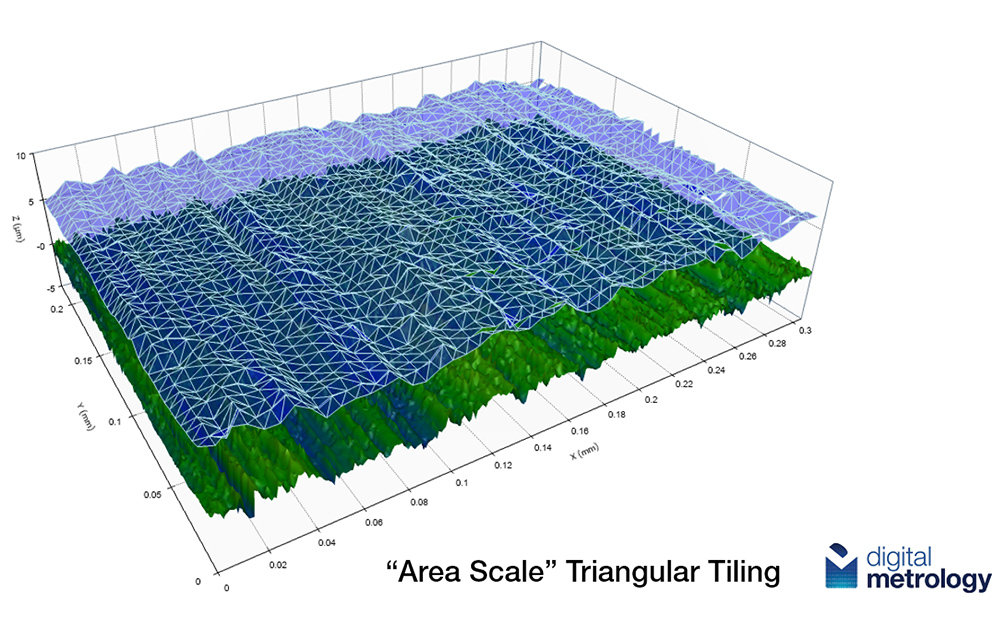
Professor Christopher Brown at Worcester Polytechnic Institute has been applying this kind of “fractal analysis” to surface measurement for last 30 years. For reference, note Christopher A. Brown, William A. Johnsen, Kevin M. Hult, Scale-sensitivity, Fractal Analysis and Simulations, Int. J. Mach. Tools Manufact. Vol 38, Nos 5-6, pp. 633-637, 1998.
Multi-scale Sdr
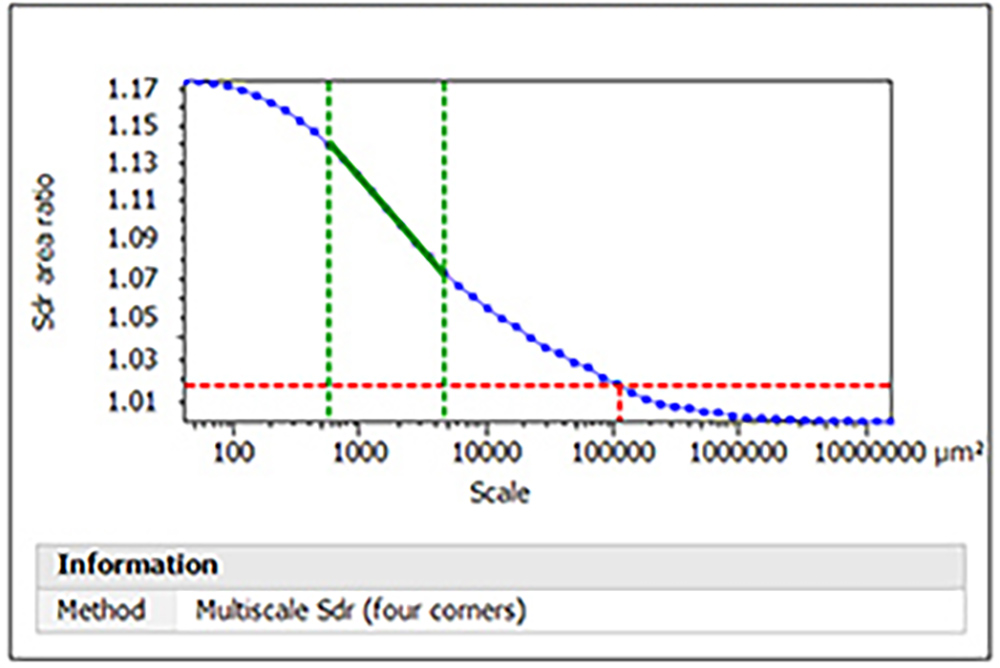
Multiscale Sdr lets us plot Sdr over a spectrum of length/area scales. In the plot below, the top/left side of the graph shows Sdr when it is calculated using the smallest area scales (i.e., the smallest possible triangles) to tile the surface. Here the Sdr equals 1.17, so the texture has added 17% to the surface area! Moving right, we calculate Sdr with progressively larger length/ area scales, until we approach the ideally smooth surface on the right side of the graph and Sdr = 1.00.
Application
Sdr may differentiate surfaces that have similar amplitudes and average roughness. Sdr is useful in applications involving surface coatings and adhesion, and when considering surfaces used with lubricants and other fluids.
Sdr can also show how various spatial wavelength bands impact the surface area. Sdr is affected both by texture amplitude and spacing. Thus, a surface dominated by longer spatial wavelengths with higher Sa may have actually a lower Sdr value than a surface comprised of short spatial wavelengths with lower Sa.
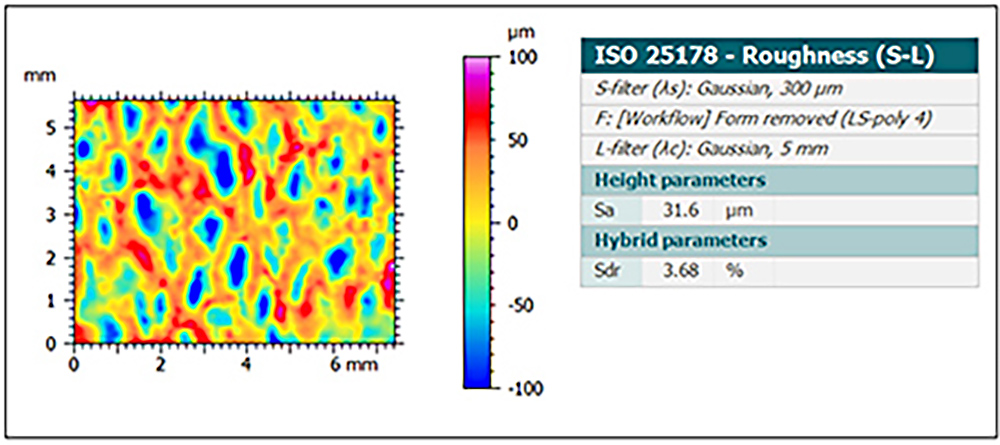
As an example, the data below shows the surface of a paper towel, as measured with a 3D optical profiler.
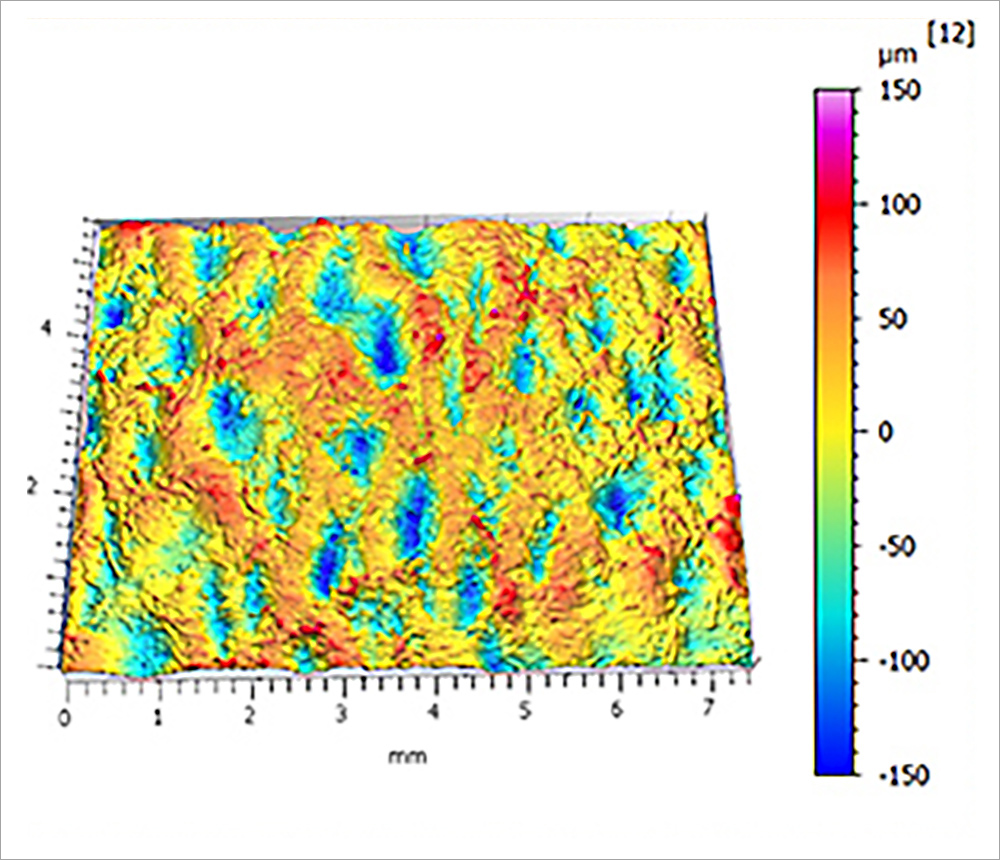
The large pores of the paper surface have spatial wavelengths between 300 µm and 5mm. These wavelengths have relatively high amplitudes, with an Sa of 31.6 µm. These large pores do increase the surface area: this wavelength band has an Sdr value of 3.68%. So, the largest pores add a little less than 4% to the surface area.
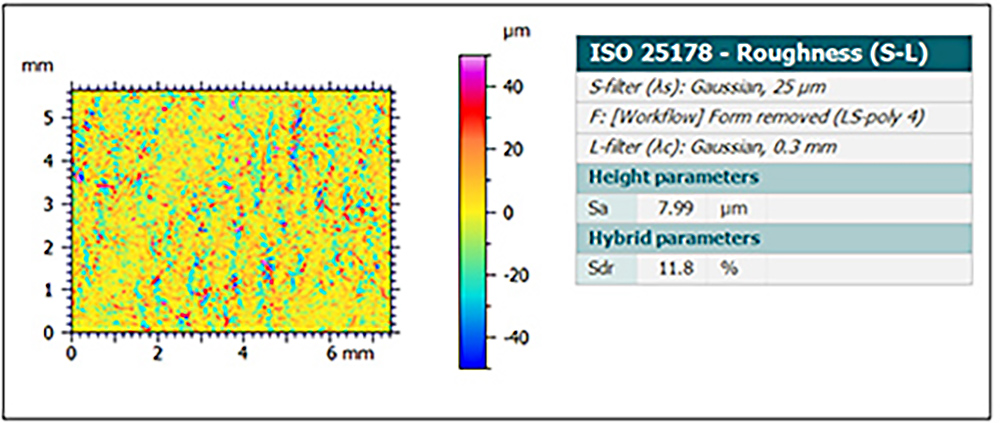
Within the larger pores, we also have smaller nooks and crannies between the paper fibers. These shorter spatial wavelength features (25–300 µm) have much lower amplitudes (Sa < 8 µm). Yet, despite their small size, these features increase the paper towel’s surface area by nearly 12%! The tiniest features increase the surface area 3 times more than the larger features. Sdr is an excellent tool for investigating these types of relationships.
Sdr applications for medical devices: What surface finish does a medical device need?
Sdr applications for coating adhesion: Which feature size scales matter for coating adhesion?
Sdr applications for lighting: What surface finish do you need for lighting applications?
